Дисперсия в статистике — что это такое и как ее вычислить

Что показывает дисперсия?

Это показатель, который отражает степень вариативности данных. Это статистический инструмент, который помогает оценить разброс в наборе. 

Если сведения колеблются вблизи среднего, то показатель будет небольшой. Если же значения сильно отличаются друг от друга, показатель возрастает. Таким образом, дисперсия в вероятности и статистике показывает:  

1. Разброс. Насколько сильно отличаются величины друг от друга.
2. Стабильность системы. Отражает, насколько однороден процесс или явление.

Представьте две компании:

• В первой все сотрудники получают около 50 тыс. рублей.  
• Во второй зарплаты варьируются от 20 до 80 тыс. рублей.  

Хотя средний доход в обеих компаниях одинаков, рассеивание во второй будет значительно выше, что указывает на большое неравенство доходов.

Кто работает с дисперсией?

С ней работают специалисты из разных сфер, от науки и до финансов. Вот кто и как использует этот показатель:

1. Аналитики и статистики. Эти специалисты превращают сухие числа в полезные инсайты. Этот способ помогает им выявлять закономерности, анализировать разброс значений и оценивать устойчивость процессов.
2. Финансовые аналитики и риск-менеджеры. Для этих профессионалов это инструмент, который позволяет измерять уровень риска и волатильности. Анализируя колебания цен на активы, они прогнозируют, насколько надежны те или иные инвестиции.
3. Экономисты. Изучают, как распределяются доходы, как развиваются регионы и насколько равномерно распределяются ресурсы.
4. Инженеры по качеству и менеджеры производств. В производстве это используется для контроля стабильности процессов и качества продукции. Чем меньше разброс, тем лучше работает процесс.
5. Ученые и исследователи. В научной деятельности показатель помогает проверять гипотезы, выявлять различия между группами информации и подтверждать статистическую значимость исследований.
6.  Социологи и маркетологи. Эти специалисты используют этот метод для понимания предпочтений и поведения аудитории. Это помогает анализировать разброс ответов респондентов, выявлять группы с общими характеристиками и разрабатывать персонализированные стратегии.
7. Разработчики искусственного интеллекта и машинного обучения. В мире технологий эта схема занимает главное место в обучении моделей. Она позволяет оценивать качество данных и помогает построить точные прогнозы.
8. Спортивные аналитики. В спорте помогает оценивать стабильность результатов спортсменов и качество их подготовки. 

Рассеивание не просто показывает разброс информации — она помогает принимать взвешенные решения в бизнесе, науке, финансах или даже в спорте. Этот инструмент делает сложные процессы прозрачными и управляемыми, позволяет специалистам видеть полную картину и находить оптимальные пути решения задач.

Когда нужно применять дисперсию?

Этот показатель помогает увидеть скрытые нюансы там, где на первый взгляд всё кажется очевидным. Его применяют, когда нужно:

1. Понять разброс значений. Если числа в таблице живут своей жизнью и их поведение непредсказуемо, расчет поможет внести ясность. Дисперсия показывает, насколько далеко одни значения уходят от других.
2. Оценить риск. Финансовые эксперты обращаются к этому методу , чтобы измерить нестабильность активов. Она служит маяком для определения рисков в инвестициях. Вкладываться в акции с большими показателями обернется выигрышем или провалом — как игра в лотерею.
3. Проверить гипотезы. Отличаются ли группы сведений друг от друга и есть ли смысл продолжать исследование или стоит искать другие подходы.
4. Контролировать процессы. Если размеры деталей отличаются, расчет это покажет и намекнет, где искать проблему.
5. Найти закономерности в хаосе. Аналитики данных обращаются к методу, чтобы упорядочить разбросанные числа и увидеть общую картину. В маркетинге с ее помощью определяют группы потребителей с похожими предпочтениями.
6. Оценить стабильность результатов.

Читайте также: В России крысу научили отвечать на вопросы по математике при помощи ИИ

Этот метод включают в работу там, где точность превращается в необходимость. Она помогает расставить акценты, увидеть правду за цифрами и принять верные решения. А теперь перейдем к тому, как искать дисперсию в статистике.

Формула дисперсии

Она позволяет вычислить, насколько данные отклоняются от своего среднего значения. Формула дисперсии в статистике выглядит так:

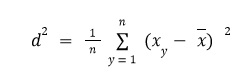
Где:  

• d2 — дисперсия (квадрат среднего отклонения).
• n — количество элементов в выборке.
• xy — каждое значение в наборе.
• x — среднее значение выборки

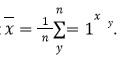
Чтобы понять, как считать дисперсию в статистике, нужно разобраться с понятием среднего значения и отклонений.

Читайте также: «Программирование — это не математика, а язык». Какие заблуждения мешают школьникам учиться

Вот как это сделать:

1. Вычисляют среднее значение x.
2. Находят разницу между каждым xyи средним x.
3. Возводят каждую разницу в квадрат (чтобы исключить влияние знака).
4. Суммируют полученные квадраты.
5. Делят результат на количество элементов n  (или  n - 1, если вычисляется выборочное рассеивание).

Для выборки вместо совокупности формула немного изменяется:

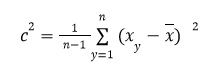
Использование n - 1 вместо n компенсирует погрешность при оценке небольшой выборки.

Пример расчета дисперсии

Как найти дисперсию в статистике?

Представьте, что вы управляете производственной линией, и вас интересует, какое время оборудование простаивает.

Есть данные: в первые три дня линии работали 2, 4 и 6 часов. Рассчитаем дисперсию, чтобы понять, насколько стабильна работа оборудования.

• Считаем среднее время работы:

х=2+4+63=4.

• Вычисляем отклонения и возводим их в квадрат:

(2 - 4)2 = 4,  (4 - 4)2 = 0,  (6 - 4)2 = 4.

• Суммируем квадраты отклонений:

4 + 0 + 4 = 8.

• Делим сумму на n (для полной совокупности):

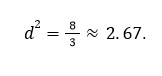
Однако для линий с высокой дисперсией стоит провести диагностику, проверить план обслуживания или пересмотреть график смен.

Расчет дисперсии в Excel 

Microsoft Excel предоставляет удобные встроенные функции для расчета. Все, что нужно — это данные и базовые знания об инструментах программы.

Рассмотрим полезные формулы:

1. =VAR.P (диапазон) 

Используют для расчета для всей совокупности информации.  

2. =VAR.S (диапазон)`  

Применяют, если рассчитывают на основе выборки (а не полной совокупности).  

Читайте также: Что не так с уроками математики и как это связано с технологической безработицей: отрывок из новой книги

Пошаговая инструкция:

1. Введите информацию в таблицу. Заполните столбец или строку значениями. Например: В ячейках A1:A5  введите данные: 2, 4, 6, 8, 10.
2. Используйте функцию. Выберите пустую ячейку, куда хотите вывести результат (например,  B1). Введите формулу: Для расчёта всей совокупности =VAR.P(A1:A5). Для расчета выборочной: =VAR.S(A1:A5) после этого нажмите Enter.
3. Получите результат. Программа автоматически вычисляет дисперсию.

Например, для информации 2, 4, 6, 8, 10 — среднее: 6.

• Для всей совокупности: 8.
• Для выборки: 10.

Если сведения динамически меняются, используйте ссылку на диапазон, чтобы результаты пересчитывались автоматически. 

Как интерпретировать результат

Определение дисперсии в статистике — это основа для понимания разброса данных и оценки их однородности. 

Вот как анализировать этот показатель:

• Значения дисперсии в статистике сильно отличаются друг от друга. 

Такой разброс указывает на нестабильность, неоднородность информации или наличие факторов, которые влияют на результат. Например, если расчет доходов сотрудников компании велик, это говорит о большом неравенстве в зарплатах.

• Значения сосредоточены вокруг среднего, различия между ними незначительны. 

Это сигнал о стабильности или равномерности. Маленькое рассеивание времени доставки товаров указывает на качественную работу логистики. Средняя дисперсия: в статистике показывает, насколько значения выборки отклоняются от среднего.

• Рассеивание выражается в квадрате исходной единицы измерения. 

Например: если сведения — в рублях, то она будет в квадратных рублях, если в секундах, результат окажется в квадратных секундах. Для удобства интерпретации используют среднеквадратическое отклонение, которое является квадратным корнем из распределения и возвращает значение в исходных единицах.

• Способ помогает сравнивать два или более набора. 

Если распределение успеваемости учеников в двух классах отличается, это говорит о том, где ученики получают стабильные оценки.

• В прикладных задачах, таких как контроль качества, низкие показатели подтверждают стабильность процесса, а высокие сигнализируют о проблемах. 

Если разброс размеров деталей велика, это указывает на необходимость калибровки оборудования.

• В финансах высокие показатели цены актива сигнализируют о волатильности (и, соответственно, риске). 

Акции с большим разбросом цен подойдут рискованным инвесторам, а с маленькой — тем, кто ищет стабильность.

Читайте также: «Вспомните, за что вы любите математику». Как подготовиться к школьной олимпиаде без потерь

Значение поможет понять поведение информации, выявить закономерности и принять обоснованные решения. Маленькие показатели говорят о предсказуемости, большие — о разнообразии или нестабильности.

Главное — рассматривать их в контексте задачи и сравнивать с реальными процессами.

Как она связана с другими статистическими показателями?

Статистические показатели позволяют компаниям принимать обоснованные решения, оптимизировать процессы и прогнозировать будущие результаты. Разберем, как каждый из этих показателей используют в бизнесе и какие выгоды он приносит:

Показатель 1. Среднеквадратическое отклонение (d)

Это квадратный корень из дисперсии:

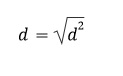
Если рассеивание показывает разброс данных в квадратных единицах, то среднеквадратическое отклонение возвращает нас к исходным единицам измерения. Это упрощает интерпретацию результата.

Например, если показатели доходов составляют 10002 рублей, то среднеквадратическое отклонение равно 31.62.

В финансах оценивают волатильность цен на акции. Например, если отклонение низкое, это свидетельствует о стабильности актива, а высокое значение указывает на риски.

Компании используют этот показатель для управления портфелем, оценки рисков и выбора стратегий инвестирования.

Показатель 2. Среднее значение х 

Разброс измеряет отклонение относительно среднего:

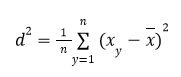
Чем ближе информация к среднему числу, тем меньше показатель, и наоборот.

Показывает центральную тенденцию данных, их «срединное значение».

Применяется в ритейле среднее значение помогает анализировать средний чек покупателя, чтобы планировать акции или оптимизировать ассортимент.

Показатель 3. Размах (Range) 

Это разница между максимальным и минимальным показателем. Его формула:

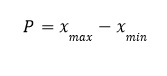
Оба показателя измеряют разброс, но размах отражает только крайние значения, а рассеивание учитывает отклонения всех сведений.

Показывает разницу между максимальным и минимальным значением.

Применяют в управлении складом, с помощью этого показателя оценивают запасы. Например, если разница между пиковыми и минимальными значениями велика, стоит пересмотреть логистику.

Показатель 4. Коэффициент вариации (CV)

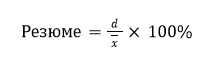
Показатель применяют в маркетинге, коэффициент вариации анализируют для оценки продуктивности рекламных кампаний в разных регионах. Если разброс высок, нужно адаптировать стратегию.

Показатель 5. Ковариация и корреляция

Показывает связь между двумя переменными.

Применяют в e-commerceс англ. «электронная коммерция». Корреляция помогает понять, какие товары чаще покупают вместе. Например, высокая корреляция между ноутбуками и аксессуарами указывает на возможность создания выгодных предложений.

В результате увеличивается оборот за счет кросс-продаж комплектов товаров.

Показатель 6. Z-оценка (стандартизация)

Показывает, насколько значение отклоняется от среднего в единицах стандартного отклонения:

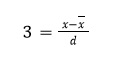
С помощью показателя можно вычислить, насколько значение отклоняется от среднего.

Применяют в анализе персонала. Z-оценка помогает выявить сотрудников с производительностью, значительно отличающейся от среднего уровня.

Эти показатели помогают бизнесу быть не только конкурентоспособным, но и устойчивым к изменениям. Они позволяют находить слабые звенья, оценивать риски и использовать ресурсы продуктивнее, делая бизнес-процессы предсказуемыми и управляемыми.

Дисперсия и отклонение в статистике играют центральную роль в анализе, помогают оценить их разброс и стабильность. Это фундаментальный показатель, который связывает разброс данных с другими характеристиками, такими как центральная тенденция, вариативность и взаимосвязь переменных. Она служит основой для анализа в статистике и помогает делать выводы о природе информации.

Фото на обложке: Freepik